Dada la ecuación de una elipse, se pueden determinar su gráfica y sus elementos desarrollando la ecuación hacia su forma canónica y sustituyendo los valores encontrados. La ecuación de la elipse de la cual vamos a encontrar esos valores es la siguiente;
La cual corresponde a la ecuación de una elipse horizontal y donde "a" elevado al cuadrado es igual a 16 y "b" elevado al cuadrado es igual a "9", por consiguiente los vértices de esta parábola se encuentran en (+-a, 0) del plano, entonces al sustituir los valores encontrados tenemos que V = (+- 4, 0) y los extremos del eje menor (0, +- 3).
A partir de estos dos valores, determinamos los focos de la la elipse. Para encontrar los focos, hacemos uso del teorema de pítagoras ("a" elevado al cuadrado es igual a la suma de "b" elevado al cuadrado mas "c" elevado al cuadrado; por lo tanto "c" elevado al cuadrado es igual a 7, entonces F ( +- la raíz cuadrada de 7, 0).
El lado rector LR es igual a 18/4 = 4 2/4 y la excentricidad es igual a la raíz cuadrada de 7 sobre 4.
Primero se transforma a su forma ordinaria pasando el termino independiente a la derecha de la igualdad; Ahora se dividen los términos a ambos lados de la igualdad entre 144 para obtener la siguiente ecuación;
A partir de estos dos valores, determinamos los focos de la la elipse. Para encontrar los focos, hacemos uso del teorema de pítagoras ("a" elevado al cuadrado es igual a la suma de "b" elevado al cuadrado mas "c" elevado al cuadrado; por lo tanto "c" elevado al cuadrado es igual a 7, entonces F ( +- la raíz cuadrada de 7, 0).
El lado rector LR es igual a 18/4 = 4 2/4 y la excentricidad es igual a la raíz cuadrada de 7 sobre 4.
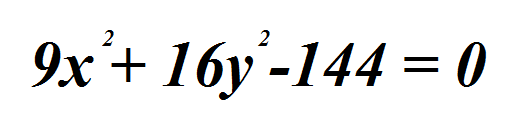


No hay comentarios:
Publicar un comentario