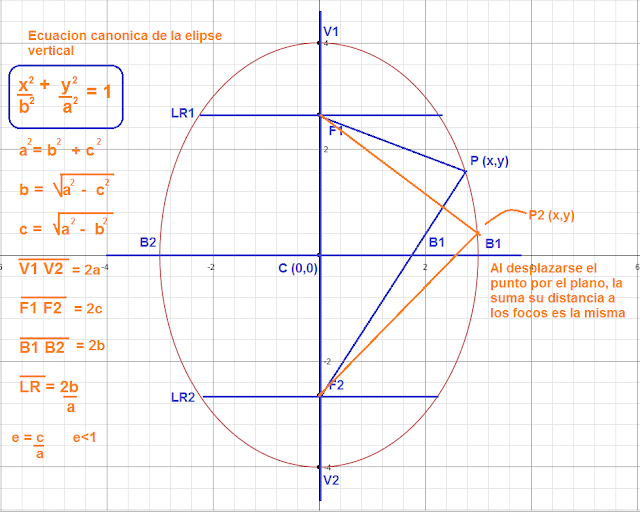
La elipse es el lugar geométrico que describe un punto que se desplaza en el plano cartesiano, tal que la suma de la distancia de este punto a dos puntos fijos "focos" es constante. Dado en punto P (x,y) en el plano, la suma de sus distancias a dos puntos fijos; F1 y F2 viene dada por PF1 + PF2 = 2a que viene siendo igual a la distancia entre los vértices; V1V2= 2a.
Si desplazamos el punto sobre el plano, la suma de las distancias sigue siendo la misma.
Matematicas faciles
Matematicas basicas
La elipse vertical cuenta con los siguientes elementos: el centro se encuentra en C = (0,0); V1 y V2 son los vértices; B1 y B2 son los extremos de eje menor; F1 y F2 son los focos; LR1 Y LR2 son los lados rectos. Por el teorema de pitagoras, "a" elevado al cuadrado es igual a "b" elevado al cuadrado mas "c" elevado al cuadrado. Las distancias de V1 a V2 = 2a de F1 a F2 = 2c, de B1 a B2 = 2b. El lado recto es igual a 2 multiplicado por "b" elevado al cuadrado y sobre "a". La excentricidad viene dada por "e" y es igual a "c" sobre "a", e es menor a 1.
Si desplazamos el punto sobre el plano, la suma de las distancias sigue siendo la misma.
Matematicas faciles
Matematicas basicas
La elipse vertical cuenta con los siguientes elementos: el centro se encuentra en C = (0,0); V1 y V2 son los vértices; B1 y B2 son los extremos de eje menor; F1 y F2 son los focos; LR1 Y LR2 son los lados rectos. Por el teorema de pitagoras, "a" elevado al cuadrado es igual a "b" elevado al cuadrado mas "c" elevado al cuadrado. Las distancias de V1 a V2 = 2a de F1 a F2 = 2c, de B1 a B2 = 2b. El lado recto es igual a 2 multiplicado por "b" elevado al cuadrado y sobre "a". La excentricidad viene dada por "e" y es igual a "c" sobre "a", e es menor a 1.

No hay comentarios:
Publicar un comentario