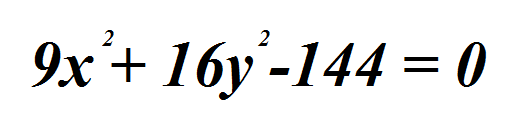Elementos de la Hipérbola Dada su Ecuación

Para obtener los elementos de la hipérbola cuya ecuación es 9x al cuadrado - 4x al cuadrado igual a , se transforma esta ecuación a si forma ordinaria dividiendo la ecuación entre el termino independiente y simplificando, la cual representa a una hipérbola horizontal; teniendo que el semieje transverso es a =2 y el semieje conjugado es B =3, con c = la raiz cuadrada de 13. A partir de estos valores se obtienen los elementos de esta hipérbola;

Ecuación de la Hipérbola Vertical con centro en el origen

La hipérbola es una figura geométrica descrita por un punto que se mueve en el plano tal que la diferencia entre este punto y dos puntos fijos llamados focos es siempre la misma;
Esta diferencia viene dada por la siguiente relación;  PF1 - PF2 = 2a, lo cual significa que la distancia descrita por un punto y uno de los focos menos la distancia entre ese mismo punto y el siguiente foco es igual a 2a (eje transverso).

En la gráfica, las parábolas verticales en rojo, representan a la hipérbola vertical con centro en el origen; las lineas discontinuas que se cortan en el centro, representan a las asintotas y es hacia estas lineas hacia donde tienden indefinidamente las lineas de la hipérbola.

La distancia comprendida entre un punto que se desplace sobre la hipérbola y un foco menos la distancia entre ese mismo punto y el siguiente foco, siempre va a dar como resultado la distancia entre los vértices de la hipérbola; V1V2 = 2a

Elementos de la hipérbola vertical;

C = centro; V1 y V2 = vertices y V1V2 = 2a; B1 y B2 = eje conjugado o imaginario y B1B2 = 2b; F1 y F2 = focos y F1F2 = 2c. LR = 2 (b al cuadrado)/a y la excentricidad viene dada por e = c/a. las asintotas son L1; y = ax/b y L1; y = -ax/b.

la ecuacion general de esta hiperbola es igual a 25y al cuadrado - 36x al cuadrado - 900 = 0 y la ecuacion ordinaria es y al cuadrado /36 - x al cuadrado/25 igual a 1 con a =6 y b =5.

Ecuacion de la Hiperbola Horizontal con Centro en el Origen

La hipérbola es el lugar geométrico descrito por un punto que se mueve en el plano tal que la diferencia entre este punto y dos puntos fijos llamados focos es siempre constante;
Esta diferencia biene dada por la siguiente relacion;  PF1 - PF2 = 2a, lo cual quiere decir que la distancia descrita por un punto y uno de los focos menos la distancia en tre ese mismo punto y el siguiente foco es igual a 2a (eje transverso).

En la grafica, las parablas horizontales en rojo, representan a la hiperbola con centro en el origen; las lineas discontinuas que se cortan en el centro, representan a las asintotas y hacia ellas tienden indefinidamente las lineas de la hiperbola.

La distancia comprendida entre un punto que se desplace sobre la hiperbola y un foco menos la distancia entre ese mismo punto y el siguiente foco, siempre va a dar como resultado la distancia entre los vertices de la hiperbola; V1V2 = 2a

Elementos de la hiperbola;

C = centro; V1 y V2 = vertices y V1V2 = 2a; B1 y B2 = eje conjugado o imaginario y B1B2 = 2b; F1 y F2 = focos y F1F2 = 2c. LR = 2 (b al cuadrado)/a y la excentricidad viene dada por e = c/a. las asintotas son L1; y = bx/a y L1; y = -bx/a.

la ecuacion general de esta hiperbola es igual a 16X al cuadrado - 25Y al cuadrado - 400 =0 y la ecuacion ordinaria es x al cuadrado /25 - y al cuadrado/16 igual a 1 con a =5 y b =4.

Determinar la gráfica de una elipse dada su ecuación general

Dada la ecuación de una elipse, se pueden determinar su gráfica y sus elementos desarrollando la ecuación hacia su forma canónica y sustituyendo los valores encontrados. La ecuación de la elipse de la cual vamos a encontrar esos valores es la siguiente;

Primero se transforma a su forma ordinaria pasando el termino independiente a la derecha de la igualdad; Ahora se dividen los términos a ambos lados de la igualdad entre 144 para obtener la siguiente ecuación;

La cual corresponde a la ecuación de una elipse horizontal y donde "a" elevado al cuadrado es igual a 16 y "b" elevado al cuadrado es igual a "9", por consiguiente los vértices de esta parábola se encuentran en (+-a, 0) del plano, entonces al sustituir los valores encontrados tenemos que V = (+- 4, 0) y  los extremos del eje menor (0, +- 3).
A partir de estos dos valores, determinamos los focos de la la elipse. Para encontrar los focos, hacemos uso del teorema de pítagoras ("a" elevado al cuadrado es igual a la suma de "b" elevado al cuadrado mas "c" elevado al cuadrado; por lo tanto "c" elevado al cuadrado es igual a  7, entonces F ( +- la raíz cuadrada de 7, 0).

El lado rector LR es igual a 18/4 = 4 2/4 y la excentricidad es igual a la raíz cuadrada de 7 sobre 4.