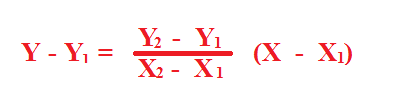Matematicas Faciles y sencillas. Numeros reales, Aritmetica, geometria, trigonometria, geometria analitica, calculo integral, calculo diferencial, matematicas financieras, economia, dinero
Java
viernes, 30 de octubre de 2015
jueves, 29 de octubre de 2015
Ecuacion Dos Puntos de una Linea Recta
Formula de la acuacion dos puntos de una linea recta
Mediante esta formula se pueden encontrar la ecuacion de la linea recta sustituyendo en la formula dos puntos (x,y) de la linea
Tomamos solo un punto de la linea recta y los sustituimos en los extremos de la formula; enseguida tomamos los dos puntos y los sustituimos en la parte derecha despues de la igualdad;
El mismo resultado se obtiene si se toma cualquier punto de la recta en el primer paso de este ejemplo
Ecuacion Punto Pendiente
La ecuacion punto pendiente es de la forma;
La solucion para esta formula se puede obtener conociendo la pendiente de una recta y cualquier punto de esa recta;
Primero obtenemos la pendiente de esta recta mediante la siguiente formula;
Ahora usamos la formula punto pendiente, insertando en la formula, "punto pendiente" cualquier punto de la linea y la pendiente de la recta;
La solucion para esta formula se puede obtener conociendo la pendiente de una recta y cualquier punto de esa recta;
Primero obtenemos la pendiente de esta recta mediante la siguiente formula;
Ahora usamos la formula punto pendiente, insertando en la formula, "punto pendiente" cualquier punto de la linea y la pendiente de la recta;
jueves, 15 de octubre de 2015
La Funcion Lineal
La funcion lineal se representa en una grafica como una linea recta. Esta funcion se puede escribir de la siguiente forma;
En donde (m) y (b) representan a dos constantes y (x) a una variable. M es la pendiente o inclinacion de la recta y b es el punto de interseccion de esta recta con el eje de las ordenadas o eje (y).
En el plano cartesiano, la ecuacion de una linea recta describe una linea con inclinacion 1/2 y que intercepta al eje de las y en 7/2.
lunes, 12 de octubre de 2015
Calculo de Logaritmos en Cualquier Base
El logaritmo de un numero X de base b se puede obtener al calcular los logaritmos de X y b con respecto a alguna otra base y utilizando la siguiente formula; (formula de cambio de base).
Comúnmente se usan logaritmos de base 10, el logaritmo binario de base 2 o el logaritmo natural de base e. Se puede utilizar cualquier otra base según convenga;
Etiquetas:
Calculo de Logaritmos en Cualquier Base,
formula de cambio de base,
logaritmo natural de base e,
logaritmos de base 10,
logaritmos de base 2
domingo, 11 de octubre de 2015
Resolviendo Ecuaciones por medio de Logaritmos
Para simplificar logaritmos mas fácilmente, nos podemos valer de algunos pasos muy simples;
1. Primero, representa a las cantidades en su forma exponencial
2. Ahora determina cual ley de los logaritmos es la mas aplicable.
Leyes de los logaritmos
Después de aplicar alguna ley de los logaritmos determina que otra ley de los logaritmos te puede ayudar a seguir simplificando la ecuación en caso de que sea muy grande;
Por ejemplo;
Aplicamos la propiedad logarítmica de los exponentes;
1. Primero, representa a las cantidades en su forma exponencial
2. Ahora determina cual ley de los logaritmos es la mas aplicable.
Leyes de los logaritmos
Después de aplicar alguna ley de los logaritmos determina que otra ley de los logaritmos te puede ayudar a seguir simplificando la ecuación en caso de que sea muy grande;
Por ejemplo;
Aplicamos la propiedad logarítmica de los exponentes;
Y por la propiedad de logaritmos con bases similares;
El logaritmo de un numero con base idéntica es 1
Ahora recurrimos al algebra para resolver;
Y al sustituir en la ecuación original;
Etiquetas:
algebra,
el logaritmo de un numero con base idéntica,
propiedad logarítmica de los exponentes,
Resolviendo Ecuaciones por medio de Logaritmos
Propiedades de los Logaritmos 6
El logaritmo de una raíz es igual al logaritmo del numero dentro del radicando dividido por el índice de la raíz;
Para demostrar esto, vamos a sustituir las variables con números reales;
La raíz la representamos como una fracción, colocando la potencia (1) del radicando como numerador y el índice como denominador;
Etiquetas:
denominador,
fracción,
índice de la raíz,
logaritmo de una raíz,
numerador,
potencia del radicando,
Propiedades de los Logaritmos 6,
radicando
sábado, 10 de octubre de 2015
Propiedades de los Logaritmos 4
El logaritmo de un cociente es igual al logaritmo del numerador
menos el logaritmo del denominador;
Por las leyes de los exponentes;
Los logaritmos se desarrollaron por su utilidad al resolver
ecuaciones. Al multiplicar dos cantidades, resulta mas sencillo usar logaritmos
para evitar operar con cantidades de varios digitos; por ejemplo, es mas facil sumar 2 + 4
que multiplicar 100 x 10,000.
Los siguientes logaritmos son de base 10;
log (100 /10000) = log (100) - log (10000)
= 2 - 4
= -2
Etiquetas:
cantidades grandes,
denominador,
ecuaciones,
leyes de los exponentes,
logaritmo de un cociente,
numerador,
Propiedades de los Logaritmos 4
Ubicación:
United States
Propiedades de los Logaritmos 3
El logaritmo de un producto es igual a la suma de los logaritmos de sus factores;
Por las leyes de los exponentes;
 |
| Mi creacion |
Ahora podemos ezscribir el logaritmo de la siguiente manera;
 |
| Mi creacion |
Etiquetas:
El logaritmo de un producto es igual a la suma de los logaritmos de sus factores,
Propiedades de lo Logaritmos 3,
reglas de los exponentes
Demostracion de las Propiedades de los Logaritmos
Propiedad de los Logaritmos 1:
Y por la ley de cociente de los exponentes:
Por la definición
de logaritmo (el logaritmo de un numero de base definida es el exponente al
cual se eleva la base para obtener una cantidad).
 |
| Mi creation |
Si tomamos a como la base de un logaritmo; el logaritmo de un numero de base a elevado a 0 es 1.
Esto se aplica a los logaritmos en cualquier base.
Esto se aplica a los logaritmos en cualquier base.
 |
| Mi creacion |
División en Notación Científica
Para dividir cantidades en notación científica, se dividen las cantidades, enseguida los exponentes de la base 10 se restan;
Para dividir numeros decimales en notación científica, se efectúa la división entre los numeros decimales, enseguida se restan los exponentes de la base 10. Por ultimo, se mutiplica el cociente decimal por la base 10 elevada a el exponente;


Etiquetas:
base 10,
cociente decimal,
exponente,
notación científica,
numeros decimales
Ubicación:
Mexico
viernes, 9 de octubre de 2015
Formula de la Distancia Entre dos Puntos
Dados dos puntos en el plano cartesiano, se puede calcular la distancia por medio de l formula de la distancia entre dos puntos;
Si le asignamos dos puntos a dos pares de coordenadas dentro del plano y después unimos esos puntos mediante una linea recta. Ahora, reemplazamos cada uno de esos pares de coordenadas dentro de la formula.
Al desarrollar la equacion obtenemos el siguiente resultado:
Etiquetas:
formula de la distancia entre dos puntos,
linea recta,
pares de coordenadas,
plano cartesiano
Ubicación:
México
jueves, 8 de octubre de 2015
Que son Los Logaritmos?
En
matemáticas, los logaritmos son la operación inversa de la
potenciacion;
El logaritmo de un numero es el exponente al cual se eleva la base para obtener un argumento (numero).
En el ejemplo anterior, a es la base; n es el exponente y x es el numero (argumento).
log2 (8) = 3
El
logaritmo de un numero X de base a es un numero n, tal que an
= X.
Si
an
= X entonces:
loga (X)
= n
De
acuerdo a esto, el logaritmo de un numero se define de la siguiente
manera;
El logaritmo de un numero es el exponente al cual se eleva la base para obtener un argumento (numero).
En el ejemplo anterior, a es la base; n es el exponente y x es el numero (argumento).
log2 (8) = 3
En
el siguiente ejemplo se ilustran los elementos de un logaritmo :
Y
esta es su forma exponencial:
Suscribirse a:
Entradas (Atom)